0-1 Knapsack w/ Backtracking

General Algorithm for backtracking

void checknode (node v) {
  node u;

  if (value(v) >= best_value) {
    best_value = value(v);
  }

  if (promising(v)) {
    for (auto c: v) {
      checknode(u);
    }
  }
}

Non-Promising Node

• 기존의 0-1 knapsack problem 에서와 마찬가지로, Non-Promising 여부를 체크하기 위해 아래 용어들을 정의합니다.

• weight: 지금까지 선택한 모든 item 들의 무게 합
• profit: 지금까지 선택된 item 들의 이익 합
• max_profit: 지금까지 계산된 profit 중 최대값

• 그리고, Backtracking 에서는 여기에 두 용어를 추가로 정의합니다.

• totweight: 지금까지의 무게합 + 추가할 수 있는 무게 총합
• bound: 지금까지의 profit + 추가할 수 있는 profit + 단위 무게로 채워넣을 수 있는 profit

• 정말 이름 그대로 bound 는, 현재 노드에서 아래로 쭉 정답을 찾아나갔을 때, 얻을 수 있는 최대 이익 을 나타냅니다.

• Non-Promising 조건들은 아래와 같습니다.

• weight 값이 상한선인 W 보다 큰가?
• 해당 노드에서의 bound 값이 현재 max profit 보다 작은가?

State Space Tree

• 그림과 함께 보면 이해가 쉬울 수 있습니다.
• 다음과 같이 아이템들이 주어졌다고 해보겠습니다.

• 그리고, 문제에서 제공한 무게 상한선 W 값은 $16$ 이라 하겠습니다.

• State Space Tree가 왼쪽 자식은 선택했음을 의미하고, 오른쪽 자식은 선택하지 않음을 의미한다고 해보겠습니다.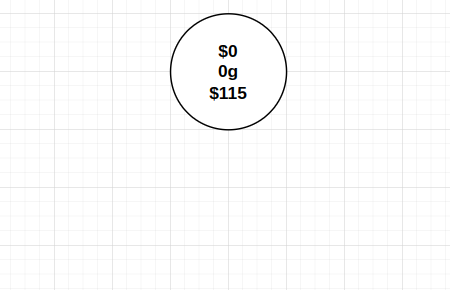

• 그럼 Root Node 는 위 그림과 같은 값을 갖게 됩니다.

• profit: $0
• weight: 0g
• bound: $0$ (현재 weight) $+ (40 + 30)$ (W를 넘지 않는 선에서의 최대 이익) $+ (16 - 7) * (50 / 10)$ (나머지 무게를 partial profit 으로 최대한 채운 값) $= 0 + 70 + 45 = 115$

• 만약 첫 번째 아이템을 선택했다면, 아래와 같은 값을 갖게 됩니다.

• profit: $40 (max profit 갱신: $40)
• weight: 2g
• bound: $40$ (현재 weight) $+ 30$ (W를 넘지 않는 선에서의 최대 이익) $+ (16 - 7) * (50 / 10)$ (나머지 무게를 partial profit 으로 최대한 채운 값) $= 40 + 30 + 45 = 115$

• 만약 두 번째 아이템을 선택하지 않는다면,

• profit: $40
• weight: 2g
• bound: $40$ (현재 weight) $+ 50$ (W를 넘지 않는 선에서의 최대 이익) $+ (16 - 12) * (10 / 5)$ (나머지 무게를 partial profit 으로 최대한 채운 값) $= 40 + 50 + 8 = 98$

• 이러한 방식으로 Backtracking 을 진행하며, 적절한 pruning 을 통해 답을 찾아갈 수 있습니다.

Algorithm

• 이를 C++ 코드로 작성하면 아래와 같습니다.

// 현재 노드에서의 profit, weight 값을 갖고 옵니다.
void knapsack(index i, int profit, int weight) {
  // 만약 무게 제한도 통과하고, maxprofit 보다 큰 이익인 상태라면
  // 정답 후보로 기록해둡니다.
  if (weight <= W && profit > maxprofit) {
    maxprofit = profit;
    best_num = i;
    // best_set 은 [1, 0, 0, 1, ...] 같은 형태로 이해하면 됩니다.
    best_set = is_include;
  }

  // promising 노드일 때, 좌우 자식에 대한 탐색 구현입니다.
  if (promising(i)) {
    is_include[i + 1] = true;
    knapsack(i+1, profit + p[i + 1], weight + w[i + 1]);

    is_include[i + 1] = false;
    knapsack(i+1, profit, weight);
  }
}

bool promising(index i) {
  index j, k;
  int totweight;
  float bound;

  // 만약 무게 한도를 초과했다면 끝입니다..
  if (weight >= W) return false;

  // bound 를 계산하는 블럭입니다.
  else {
    j = i + 1;
    bound = profit;
    totweight = weight;

    // 일단 무게 한도 내에서 추가할 수 있는 최대한 추가 해봅니다.
    while (j <= n && totweight + w[j] <= W) {
      totweight += w[j];
      bound += p[j];
      j++;
    }

    // 남은 무게 공간은 partial profit 으로 채웁니다.
    k = j;
    if (k <= n) {
      bound += (W-totweight) * (p[k]/w[k]);
    }

    // 만약 bound 값이 maxprofit 보다 작다면 끝입니다..
    return bound > maxprofit;
  }
}

Ref

• blog